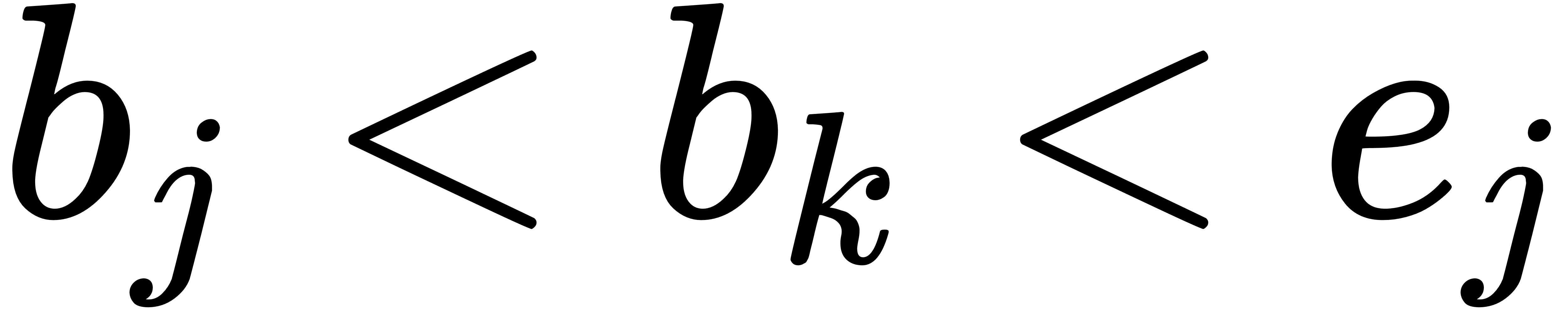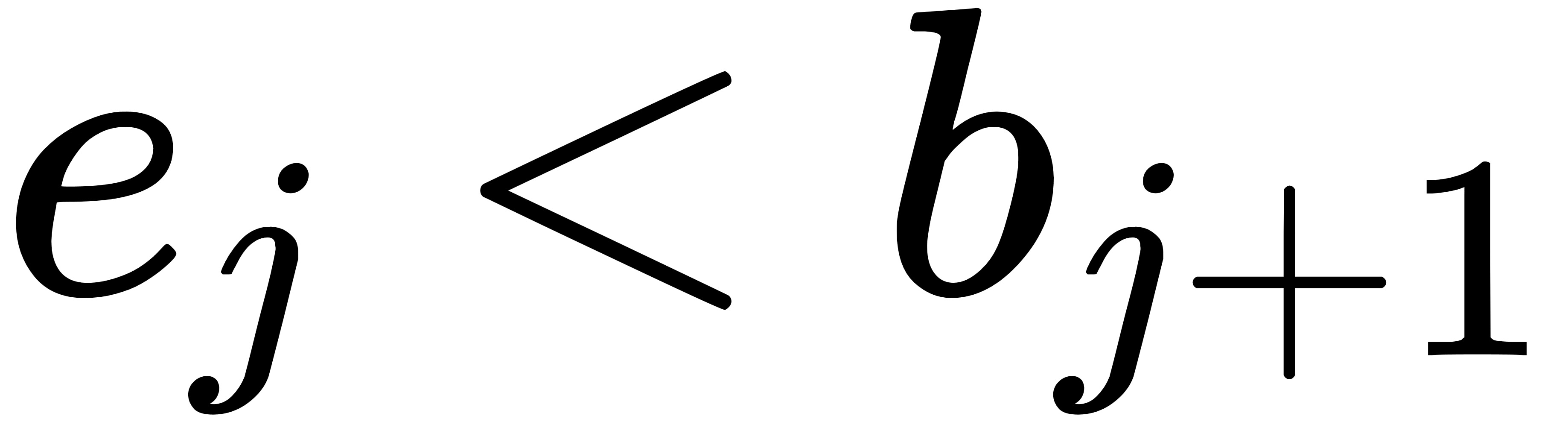如何检查一组区间中是否存在两个区间有交集(新)
序言
假设有 N 个区间,每一个都可以表示为
如果要判断这些区间中是否存在两个之间是有重叠的,可以采用下面的算法:
- 将所有的区间按照各自的下确界递增排列;
- 如果相邻的区间不会重叠,则所有的区间都不会重叠。否则,存在区间重叠。
尽管这个算法非常符合直觉,但会不会存在两个不相邻的区间反而是重叠的呢?答案是否定的,接下来给出证明。
算法证明
首先对这些区间进行排序,使得排序后的所有区间都满足下列关系
接下来采用反证法,即:尽管所有相邻的区间都不会重叠,但仍然存在两个不相邻的区间是重叠的。假设第 j 个和第 k 个区间有重叠,不妨假设 j 小于 k,则它们满足如下关系
由于相邻的区间不重叠,因此就有
由于 k 不是 j 的相邻区间,因此 k 大于 j 加上 1,结合上面两个不等式可以得到
这与一开始所有区间排序后所满足的关系矛盾,因此假设不成立,即:不存在两个不相邻的区间是有重叠的。