递归、闭包、面向对象
话题由来
参加了不少IT公司的笔试,有些题目遇到的次数还是比较多的,例如给一系列字符和一个空栈,询问你选项中的哪一个是不可能出现的出栈顺序这样的问题。另外一道题目,就是我这里要拿来讲的,不过我讲的和题目本身不直接相关,只是恰好和题目所要完成的任务有重合罢了。这道题目就是“给出一颗二叉树的先序遍历和中序遍历的输出结果,请给出这个二叉树的后序遍历的输出结果”。
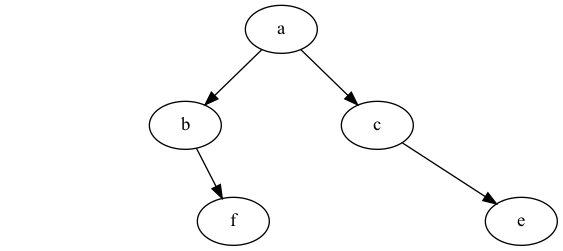
这道题目其实非常简单,尽管我一开始遇到的时候仍然是手足无措的(谁没有年少无知过呢对不),不过一两次之后就轻车熟路了,知道了这样的题目的行之有效的解法。举个例子,先序的序列和中序的序列分别是"abfce"和"bface",那么这棵二叉树就是这样子的
可以知道,后序遍历的输出结果为"fbeca"。怎么得到这棵二叉树呢?其实很简单,首先根据先序遍历的定义,所以在先序遍历结果中的第一个元素一定是整棵二叉树的根结点,也就是a,那么根据中序遍历的定义,在a左边出现的序列就是左子树的中序遍历结果,在a的右边的就是右子树的中序遍历结果,它们分别是"bf"和"ce"。并且可以知道,在先序遍历中与它们对应的片段应该也是"bf"和"ce"。在对"bf"做同样的处理,就可以知道b是根结点,而左子树为空且右子树为单节点f,另一棵子树的根结点为c且左子树为空,右子树为单节点e。
那么,怎么用程序来自动化呢?
C语言的递归版本
以文字来描述根据先序和中序来构造二叉树的算法还是很好理解的。为了描述方便,取几个名字。把先序遍历的结果叫做preseq,中序遍历的输出结果叫做inseq,并且把它们当作C语言中的数组那样来取出元素(例如preseq[0]表示第一个元素),再给它们一个方便取出片段的语法糖,例如preseq[0..2]表示取出下标从0到2的三个元素组成一个新的输出序列。
首先,取出preseq的第一个元素preseq[0],可以知道它肯定是目前正在处理的整棵二叉树的根结点,接着在inseq中寻找这个根结点,于是就可以把inseq分成三段,第一段是左子树的中序输出结果inseq1,第二段是根结点本身inseq2,第三段则是右子树的中序输出结果inseq3。同样的,preseq也可以分成三部分:第一个元素就是根结点,记为preseq1,然后是和inseq1等长的一个子串,也就是左子树的先序遍历的输出结果,剩下的,就是和inseq3等长的子串,即右子树的先序遍历输出结果了。既然有得到了先序和中序遍历的输出结果各一对,那么接下来只要对对应的一对输出结果递归调用原来的功能就可以了。递归的base case,就是输出结果只有一个元素的情况。这时候只需要生成一个没有左右子树的节点即可。
我写了两个版本,第一个是很简单很直接的实现,就是完全按照上面所说的思路来做的,因此其中充满了字符串的复制操作,详见代码(其中的make_tree_by_prein函数就是实现了上面的算法的代码)
/*
* postorder_output.c
*
* Generates a binary tree according to the two outputs of preorder and
* inorder traversal and outputs a sequence of nodes by postorder traversal.
*
* Copyright (C) 2012-10-25 liutos <mat.liutos@gmail.com>
*/
#include <stdlib.h>
#include <string.h>
#include <stdio.h>
struct treeNode;
typedef struct treeNode *TreeNode;
typedef TreeNode Tree;
struct treeNode {
char value;
Tree left, right;
};
TreeNode make_node(char value, Tree left, Tree right)
{
TreeNode node = malloc(sizeof(struct treeNode));
node->value = value;
node->left = left;
node->right = right;
return node;
}
/* Find the position of a character in a string. */
int find_position(char c, char *string)
{
int i;
for (i = 0; string[i] != '\0'; ++i) {
if (string[i] == c) {
return i;
}
}
return -1;
}
char *safe_strndup(char *s, int n)
{
char *str = strndup(s, n + 1);
str[n] = '\0';
return str;
}
Tree make_tree_by_prein(char *preseq, char *inseq)
/* Assumes that the `preseq' and `inseq' is correct completely. */
{
if (NULL == preseq)
return NULL;
if ('\0' == preseq[1])
return make_node(preseq[0], NULL, NULL);
else {
char root_value = *preseq;
int position = find_position(root_value, inseq);
char *left_pre; /* The output in preorder of left subtree. */
char *left_in; /* The output in inorder of left subtree. */
char *right_pre; /* The output in preorder of right subtree. */
char *right_in; /* The output in inorder of right subtree. */
left_pre = safe_strndup(preseq + 1, position);
left_in = safe_strndup(inseq, position);
right_pre = strdup(preseq + position + 1);
right_in = strdup(inseq + position + 1);
return make_node(root_value,
make_tree_by_prein(left_pre, left_in),
make_tree_by_prein(right_pre, right_in));
}
}
void print_tree(Tree tree)
{
if (tree != NULL) {
print_tree(tree->left);
print_tree(tree->right);
printf("%c", tree->value);
}
}
int main(int argc, char *argv[])
{
print_tree(make_tree_by_prein("abdfgceh", "dbgfaceh"));
putchar('\n');
return 0;
}第二个版本避免了字符串的复制操作,不过没有第一个版本的make_tree_by_prein函数那么好理解了。这里只有修改后的make_tree_by_prein函数的代码
Tree make_tree_aux(char *preseq, int sp, int ep, char *inseq, int si, int ei)
{
if (NULL == preseq || sp > ep)
return NULL;
if (sp == ep)
return make_node(preseq[sp], NULL, NULL);
else {
char root_value = preseq[sp];
int offset = find_position(root_value, inseq + si); /* The `offset' must not greater than the difference between `ep' and `sp'. */
Tree left = make_tree_aux(preseq, sp + 1, sp + offset,
inseq, si, si + offset - 1);
Tree right = make_tree_aux(preseq, sp + offset + 1, ep,
inseq, si + offset + 1, ei);
return make_node(root_value, left, right);
}
}
Tree make_tree_by_prein(char *preseq, char *inseq)
/* Second version. Avoid the duplication of many substrings. */
{
return make_tree_aux(preseq, 0, strlen(preseq) - 1,
inseq, 0, strlen(inseq) - 1);
}CommonLisp和Java的版本
C语言中的第二个版本在CommonLisp和Java里面可以改得更好一点,这多亏了CommonLisp的闭包特性和Java的OO方式。在C实现的第二个版本中,make_tree_by_prein函数有两个参数,而辅助函数make_tree_aux则需要两个参数。其中参数preseq和inseq是两个在传递过程中完成不会被修改的参数,它们之所以被作为参数,仅仅是因为C语言中只有两种方式在函数间共享一些信息:
- 函数参数
- 全局变量
因为不想使用全局变量,所以只好在参数列表中动手脚了,不过在CommonLisp和Java的实现,就有办法可以在函数之间以受控的方式共享信息。例如下面用CommonLisp实现的make-tree-by-prein函数
;;;; The Common Lisp version implementation of the function implemented previously in C
;;; A non-trivial implementation
(defun make-tree-by-prein (preseq inseq)
(labels ((aux (sp ep si ei)
(cond ((> sp ep) nil)
((= sp ep) (make-tree-node (char preseq sp) nil nil))
(t
(let* ((root-value (char preseq sp))
(offset (position root-value inseq :start si))
(left (aux (1+ sp) (+ sp offset)
si (+ si offset -1)))
(right (aux (+ sp offset 1) ep
(+ si offset 1) ei)))
(make-tree-node root-value left right))))))
(aux 0 (1- (length preseq)) 0 (1- (length inseq)))))函数make-tree-by-prein利用labels在函数体内部定义了一个闭包aux,preseq和inseq则是在词法范围内可见的变量,因为在aux内部依然可以访问到它们,这样就不需要将它们作为aux的两个参数来进行传递了。而Java的实现也是类似的,在Java中方法从属于类,并且它们可以共享同一个类的实例中的所有变量,因此直接使用这些变量即可,代码如下(因为Java同样没有办法定义内部函数的关系,所以只好定义一个用private修饰的方法makeTreeAux了。)
/*
* TreePost.java
*
*
*
* Copyright (C) 2012-10-25 liutos
*/
class TreeNode
{
char value;
TreeNode left, right;
public TreeNode(char value, TreeNode left, TreeNode right)
{
this.value = value;
this.left = left;
this.right =right;
}
void postorderPrintTree()
{
postorderPrintTreeAux(this);
System.out.println("");
}
void postorderPrintTreeAux(TreeNode tree)
{
if (tree != null) {
postorderPrintTreeAux(tree.left);
postorderPrintTreeAux(tree.right);
System.out.print(tree.value);
}
}
}
public class TreePost
{
String preseq, inseq;
public static void main(String[] args)
{
TreePost tp = new TreePost("abfce", "bface");
TreeNode tree = tp.makeTree();
tree.postorderPrintTree();
}
public TreePost(String preseq, String inseq)
{
this.preseq = preseq;
this.inseq = inseq;
}
public TreeNode makeTree()
{
return makeTreeAux(0, preseq.length() - 1, 0, inseq.length() - 1);
}
private TreeNode makeTreeAux(int sp, int ep, int si, int ei)
{
if (sp > ep) return null;
// System.out.println("Processing " + preseq.substring(sp, ep + 1) + " and " + inseq.substring(si, ei + 1));
if (sp == ep) {
System.out.println("One character " + preseq.charAt(sp));
return new TreeNode(preseq.charAt(sp), null, null);
} else {
char rootValue = preseq.charAt(sp);
int offset = inseq.indexOf(rootValue, si); // This `offset' is a offset to the beginning of string `inseq', so the rest use of this variable must minus the variable `si'.
TreeNode left = makeTreeAux(sp + 1, sp + offset - si, si, si + offset - si - 1);
TreeNode right = makeTreeAux(sp + offset - si + 1, ep, si + offset - si + 1, ei);
return new TreeNode(rootValue, left, right);
}
}
}不是有人说吗?OO是穷人的闭包;闭包是穷人的OO;-)
后记
总算把讲思路贴代码的东西弄完了,可以好好扯淡一番了=。=话说上课的时候有个考研的同学找我讲话(班里的一名胖子,在算法方面有很厉害的嗅觉),就是问我对于用算法来实现“根据先序和中序输出结果如何构造二叉树”有没有思路。递归的方法其实很容易就可以想出来了,加之我之前已经想过这类题目要怎么系统地解决,所以很快就说出来了。然后我就觉得用C语言可以像上面那样写出一个高效(即没什么字符串复制操作)的版本,接着又想到这个可以用Lisp(或者其它带闭包的语言)来实现得更好,又想到了用Java也可以实现闭包的那类效果,再接着又觉得可以发篇文章来讨论讨论,于是就有这样的一篇东西了。
对于具体实现某个功能的技术,我貌似没有特别地挑剔,甚至可以说,对于加入到编程语言中的任何特性,我都没有太挑剔的,只要好用,那么我就很可能会接纳——当然了,我也无法保证自己在找到一个反例之后不会把这句话给改掉当作自己没有这么说过,不过暂时没有想到这种情况,所以就先当作我是这样的人吧。举个例子,对于Haskell我很喜欢,也很喜欢纯函数语言的说法,即“纯函数是非常有利于程序编写的”。不过对于副作用我也没有持完全拒绝的态度,即使我在编程的过程中也会尽量遵循函数式编程的规矩(尽量避免副作用)。可是副作用实际上避无可避,倒不如拥抱它们。或许正是因为这个原因,我才会喜欢OCaml更甚于Haskell吧——至少目前是这样的。
我也喜欢惰性计算,尤其是其带来的效果——无限长的列表推到看起来实在是帅得不行,并且还可以使得编写的程序拥有了函数式的外观和命令式的效率(例如《SICP》中举的例子,用惰性计算结合map、filter和reduce)。拥有惰性计算有利无害,何乐而不为呢~或许也正是因为自己对特性的需求是多多益善,所以才喜欢Common Lisp吧。